1	这是崔斯特的第七十三篇原创文章

深度学习 (๑• . •๑)

神经网络定义

人工神经网络，简称神经网络，在机器学习和认知科学领域，是一种模仿生物神经网络（动物的中枢神经系统，特别是大脑）的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。

为了描述神经网络，我们先从最简单的神经网络讲起，这个神经网络仅由一个“神经元”构成，以下即是这个“神经元”的图示：

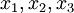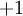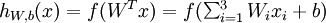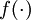
这个“神经元”是一个以 $\textstyle x_1, x_2, x_3$ 及截距 $\textstyle +1$ 为输入值的运算单元，其输出为 $\textstyle h_{W,b}(x) = f(W^Tx) = f(\sum_{i=1}^3 W_{i}x_i +b)$ ，其中函数 $\textstyle f : \Re \mapsto \Re$ 被称为“激活函数”。在本教程中，我们选用sigmoid函数作为激活函数 $\textstyle f(\cdot)$

可以看出，这个单一“神经元”的输入－输出映射关系其实就是一个逻辑回归（logistic regression）。

神经网络模型

所谓神经网络就是将许多个单一“神经元”联结在一起，这样，一个“神经元”的输出就可以是另一个“神经元”的输入。例如，下图就是一个简单的神经网络：

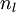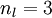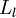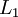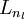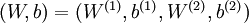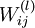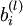我们用 $\textstyle {n}_l$ 来表示网络的层数，本例中 $\textstyle n_l=3$ ，我们将第 $\textstyle l$ 层记为 $\textstyle L_l$ ，于是 $\textstyle L_1$ 是输入层，输出层是 $\textstyle L_{n_l}$ 。本例神经网络有参数 $\textstyle (W,b) = (W^{(1)}, b^{(1)}, W^{(2)}, b^{(2)})$ ，其中 $\textstyle W^{(l)}_{ij}$ （下面的式子中用到）是第 $\textstyle l$ 层第 $\textstyle j$ 单元与第 $\textstyle l+1$ 层第 $\textstyle i$ 单元之间的联接参数（其实就是连接线上的权重，注意标号顺序）， $\textstyle b^{(l)}_i$ 是第 $\textstyle l+1$ 层第 $\textstyle i$ 单元的偏置项。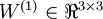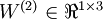因此在本例中， $\textstyle W^{(1)} \in \Re^{3\times 3}$ ， $\textstyle W^{(2)} \in \Re^{1\times 3}$ 。注意，没有其他单元连向偏置单元(即偏置单元没有输入)，因为它们总是输出 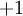$\textstyle +1$ 。同时，我们用 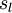$\textstyle s_l$ 表示第 $\textstyle l$ 层的节点数（偏置单元不计在内）。

Keras实战

使用keras实现如下网络结构, 并训练模型:

使用场景:

输入值(x1,x2,x3)代表人的身高体重和年龄, 输出值(y1,y2)

import numpy as np
# 总人数是1000, 一半是男生
n = 1000
# 所有的身体指标数据都是标准化数据, 平均值0, 标准差1
tizhong = np.random.normal(size = n) 
shengao = np.random.normal(size=n)
nianling = np.random.normal(size=n)
# 性别数据, 前500名学生是男生, 用数字1表示
gender = np.zeros(n)
gender[:500] = 1
# 男生的体重比较重,所以让男生的体重+1
tizhong[:500] += 1
# 男生的身高比较高, 所以让男生的升高 + 1
shengao[:500] += 1
# 男生的年龄偏小, 所以让男生年龄降低 1
nianling[:500] -= 1

创建模型


from keras import Sequential
from keras.layers import Dense, Activation
model = Sequential()
# 只有一个神经元, 三个输入数值
model.add(Dense(4, input_dim=3, kernel_initializer='random_normal', name="Dense1"))
# 激活函数使用softmax
model.add(Activation('relu', name="hidden"))
# 添加输出层
model.add(Dense(2, input_dim=4, kernel_initializer='random_normal', name="Dense2"))
# 激活函数使用softmax
model.add(Activation('softmax', name="output"))

编译模型

需要指定优化器和损失函数:

1
2
3

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

训练模型

# 转换成one-hot格式
from keras import utils
gender_one_hot = utils.to_categorical(gender, num_classes=2)
# 身体指标都放入一个矩阵data 
data = np.array([tizhong, shengao, nianling]).T
# 训练模型
model.fit(data, gender_one_hot, epochs=10, batch_size=8)

输出(stream):
Epoch 1/10
1000/1000 [==============================] - 0s 235us/step - loss: 0.6743 - acc: 0.7180
Epoch 2/10
1000/1000 [==============================] - 0s 86us/step - loss: 0.6162 - acc: 0.7310
Epoch 3/10
1000/1000 [==============================] - 0s 88us/step - loss: 0.5592 - acc: 0.7570
Epoch 4/10
1000/1000 [==============================] - 0s 87us/step - loss: 0.5162 - acc: 0.7680
Epoch 5/10
1000/1000 [==============================] - 0s 89us/step - loss: 0.4867 - acc: 0.7770
Epoch 6/10
1000/1000 [==============================] - 0s 88us/step - loss: 0.4663 - acc: 0.7830
Epoch 7/10
1000/1000 [==============================] - 0s 87us/step - loss: 0.4539 - acc: 0.7890
Epoch 8/10
1000/1000 [==============================] - 0s 86us/step - loss: 0.4469 - acc: 0.7920
Epoch 9/10
1000/1000 [==============================] - 0s 88us/step - loss: 0.4431 - acc: 0.7940
Epoch 10/10
1000/1000 [==============================] - 0s 88us/step - loss: 0.4407 - acc: 0.7900
输出(plain):

进行预测

test_data = np.array([[0, 0, 0]])
probability = model.predict(test_data)
if probability[0, 0]>0.5:
    print('女生')
else:
    print('男生')

1 2	输出(stream): 女生

关键词解释

input_dim: 输入的维度数
kernel_initializer: 数值初始化方法, 通常是正太分布
batch_size: 一次训练中, 样本数据被分割成多个小份, 每一小份包含的样本数叫做batch_size
epochs: 如果说将所有数据训练一次叫做一轮的话。epochs决定了总共进行几轮训练。
optimizer: 优化器, 可以理解为求梯度的方法
loss: 损失函数, 可以理解为用于衡量估计值和观察值之间的差距, 差距越小, loss越小
metrics: 类似loss, 只是metrics不参与梯度计算, 只是一个衡量算法准确性的指标, 分类模型就用accuracy