Fork me on GitHub

Leetcode 287. 寻找重复数

发表于 | 分类于 
这是崔斯特的第一百零二篇原创文章

努力、奋斗

题目描述

给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

示例1：

1
2
输入: [1,3,4,2,2]
输出: 2

示例2：

1
2
输入: [3,1,3,4,2]
输出: 3

说明：

1
2
3
4
不能更改原数组（假设数组是只读的）。
只能使用额外的 O(1) 的空间。
时间复杂度小于 O(n2) 。
数组中只有一个重复的数字，但它可能不止重复出现一次。

解题思路

二分法

思路是采用了二分法+抽屉原理。首先解释一下为什么用二分法，因为O(n2)时间复杂度不能A，所以往下应该是n*logn，很容易联想到二分法，因为其复杂度为logn。

抽屉原理是说假设你有11个苹果，要放进10个抽屉，那么至少有一个抽屉里是有两个苹果的。

对应到这题，1~n的n+1个数字，有1个数字会至少重复两次。

比如取数组为｛1，2，2，3，4，5｝，一共6个数，范围是1~5，其中位数应该是（5+1）/2 = 3，那么，如果小于等于3的数的个数如果超过了3，那么重复的数字一定出现在[1，3]之间，否则出现在[4，5]之间。以该数组为例，中位数为3，小于等于3的数一共有4个，大于3的数有两个，所以重复的数字在[1,3]之间。

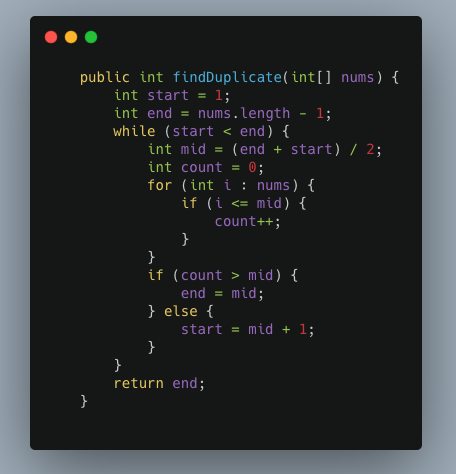
JAVA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Solution {
    public int findDuplicate(int[] nums) {
        int start = 1;
        int end = nums.length - 1;
        while (start < end) {
            int mid = (end + start) / 2;
            int count = 0;
            for (int i : nums) {
                if (i <= mid) {
                    count++;
                }
            }
            if (count > mid) {
                end = mid;
            } else {
                start = mid + 1;
            }
        }
        return end;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        left, right = 1, len(nums) - 1
        while left < right:
            mid = (left + right) // 2
            count = sum(i <= mid for i in nums)
            if count > mid:
                right = mid
            else:
                left = mid + 1
        return right

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func findDuplicate(nums []int) int {
	start, end := 1, len(nums)-1
	for start < end {
		mid := (start + end) / 2
		count := 0
		for _, v := range nums {
			if v <= mid {
				count++
			}
		}
		if count > mid {
			end = mid
		} else {
			start = mid + 1
		}
	}
	return start
}

快慢指针

数组的索引与存储的数值之间形成了特殊链表。

如果存在重复的数，因为数组大小是 n+1，数字范围是1~n，所以该链表存在环。

环的入口即为结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int findDuplicate(int[] nums) {
        // 快慢指针
        int fast = nums[0];
        int low = nums[0];
        do{
            low = nums[low];
            fast = nums[nums[fast]];
        }while(fast != low);
        int step = nums[0];
        // 寻找环链表的入口，即为结果
        while(step != low){
            step = nums[step];
            low = nums[low];
        }
        return low;
    }
}

现在还没看懂这种方法